- どのような学問? 学問の解説
- 何がポイント? 学びの特色
- どのように学ぶ? カリキュラムの体系
- 卒業後の進路は? 主な就職・進路先
どのような学問? 学問の解説
論理的思考力と、問題の発見・解決能力を身に付ける。社会や企業が求める人材へ成長していく。
「数学が好き」という人にとって、数学ほど面白い知的ゲームはなく、応用数学科では数学に純粋に取り組むことができます。
その一方で、あらゆる科学の基礎を支えているのも数学です。高度な数学を専門的に学ぶことで養われる論理的な思考力、問題の本質を見極め解決する力は、社会や企業が求めている能力にほかなりません。
このように有為な人材への成長が果たせるのも「数学を学び、数学で高まる」をテーマとする本学科ならではです。
応用数学科に社会数理・情報インスティテュートがあります。
理学部(社会数理・情報インスティテュート)個別サイト
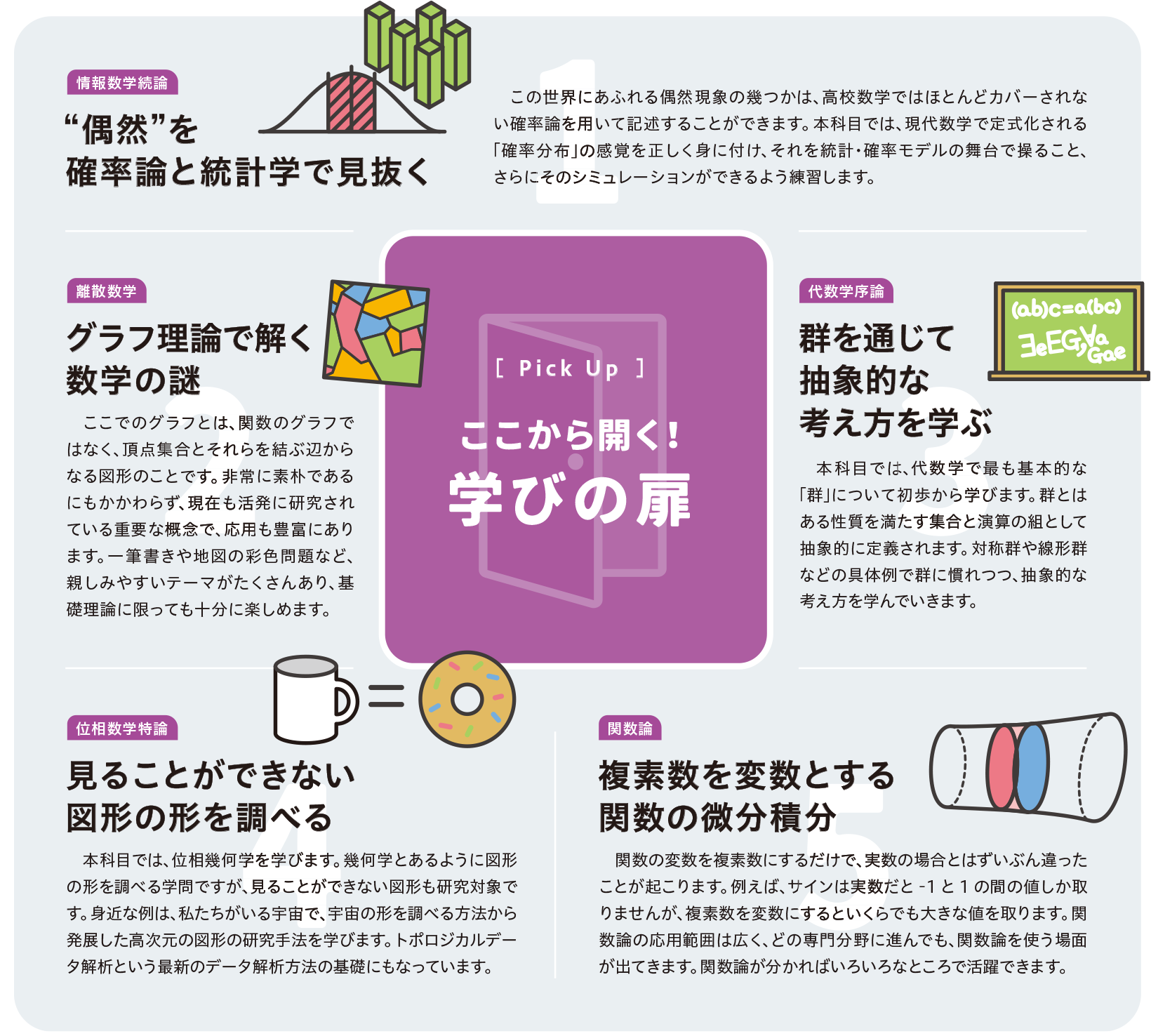
 [ Pick Up ]ここから開く!学びの扉
[ Pick Up ]ここから開く!学びの扉
情報数学続論
“偶然”を確率論と統計学で見抜く

この世界にあふれる偶然現象の幾つかは、高校数学ではほとんどカバーされない確率論を用いて記述することができます。本科目では、現代数学で定式化される「確率分布」の感覚を正しく身に付け、それを統計・確率モデルの舞台で操ること、さらにそのシミュレーションができるよう練習します。
離散数学
グラフ理論で解く数学の謎

ここでのグラフとは、関数のグラフではなく、頂点集合とそれらを結ぶ辺からなる図形のことです。非常に素朴であるにもかかわらず、現在も活発に研究されている重要な概念で、応用も豊富にあります。一筆書きや地図の彩色問題など、親しみやすいテーマがたくさんあり、基礎理論に限っても十分に楽しめます。
代数学序論
群を通じて抽象的な考え方を学ぶ

本科目では、代数学で最も基本的な「群」について初歩から学びます。群とはある性質を満たす集合と演算の組として抽象的に定義されます。対称群や線形群などの具体例で群に慣れつつ、抽象的な考え方を学んでいきます。
位相数学特論
見ることができない図形の形を調べる

本科目では、位相幾何学を学びます。幾何学とあるように図形の形を調べる学問ですが、見ることができない図形も研究対象です。身近な例は、私たちがいる宇宙で、宇宙の形を調べる方法から発展した高次元の図形の研究手法を学びます。トポロジカルデータ解析という最新のデータ解析方法の基礎にもなっています。
関数論
複素数を変数とする関数の微分積分
関数の変数を複素数にするだけで、実数の場合とはずいぶん違ったことが起こります。例えば、サインは実数だと -1 と 1 の間の値しか取りませんが、複素数を変数にするといくらでも大きな値を取ります。関数論の応用範囲は広く、どの専門分野に進んでも、関数論を使う場面が出てきます。関数論が分かればいろいろなところで活躍できます。
在学生の声
卒業生の声
関連リンク
- どのような学問? 学問の解説
- 何がポイント? 学びの特色
- どのように学ぶ? カリキュラムの体系
- 卒業後の進路は? 主な就職・進路先



